Wahrscheinlichkeitsräume

Definition 1: Wahrscheinlichkeitsraum

Ein (diskreter [1]) Wahrscheinlichkeitsraum ist eine Ergebnissmenge \(\Omega = \{\omega_1, \omega_2\, \omega_3, ...\}\) [2] von Elementarerignissen \(\omega_1, \omega_2\, \omega_3, ...\) . Jedem \(\omega_i\) ist eine Wahrscheinlichkeit \(Pr[\omega_i]\) zugeordnet, so dass gilt:

• \(0\le Pr[\omega_i] \le 1\)
• \(\sum_{\omega_i\in \Omega} Pr[\omega_i] = 1\)

Definition 2: Ereignis

Die Wahrscheinlichkeit von Ereignis \(E\subseteq\Omega\) ist:

\[Pr[E] = \sum_{\omega\in E} Pr[\omega]\]

Ein Ereignis E tritt ein, wenn eines der Elementarereignissen aus E eintritt.

Speziell:

• \(\emptyset\) - das unmögliche Ereignis
• \(\Omega\) - das sichere Ereignis

Definition 3: Komplementär Ereignis

Das komplementäre Ereignis zu E ist \(\bar E=\Omega-E\).

Definition 4: Relative Häufigkeit bzw. Wahrscheinlichkeit

Statistik über die Häufigkeit von Ereignis E.

Relative Häufigkeit (E) \(=\frac{absolute Häufigkeit (E)}{Anzahl Messungen}\)

Relative Häufigkeiten gelten als Erwartungen für die Zukunft und können als Wahrscheinlichkeiten (Wk., en: propability) betrachtet werden.

Für die Wahrscheinlichkeit eines Ereignisses E, werden die Wahrscheinlichkeiten der Elementarereignissen in E aufsummiert.

Definition 5: Laplace Experiment:

Alle Elementarereignisse \(\omega_i\) einer endlichen Ergebnismenge \(\Omega\) sind gleich wahrscheinlich.

\[Pr[\omega]=\frac{1}{\vert\Omega\vert}, \;\; \forall\omega\in\Omega\]

Allgemein für ein Ereignis E:

\[Pr[E]=\frac{\vert E\vert}{\vert\Omega\vert}\]

Lemma:

\(0\le\frac{1}{\vert\Omega\vert}\le 1\) und

\(\sum_{\omega\in\Omega}Pr[\omega]=\sum_{\omega\in\Omega}\frac{1}{\vert\Omega\vert}= \frac{1}{\vert\Omega\vert}\sum_{\omega\in\Omega}1=\frac{1}{\vert\Omega\vert} * \vert\Omega\vert = 1\)

Beispiele:

1. Würfel (Laplace Experiment)

   \(\Omega=\{1,2,3,4,5,6\}\)

   \(Pr[k]=\frac{1}{6}\) mit \(1\le k\le 6\)

   Ereignis \(P=\{k\in\Omega\mid k\; ist\; prim\} = \{2,3,5\}\)

   \(Pr[P]=3*\frac{1}{6}=\frac{1}{2}\)

2. Münze: 3-mal werfen (Laplace Experiment)

   \(\Omega=\{k,z\}^3\) , \(\vert\Omega\vert = 8\)

   \(Pr[\omega]=\frac{1}{8}\)

   E = genau einmal k

   \(Pr[E]=3*\frac{1}{8}=\frac{3}{8}\)

3. Urne:

   5 Bälle, 2 rot (r) und 3 schwarz (s)

   Ziehe 2 mal ohne Zurücklegen.

   \(\Omega=\{r,s\}^2\) , \(\vert\Omega\vert = 4\)

   

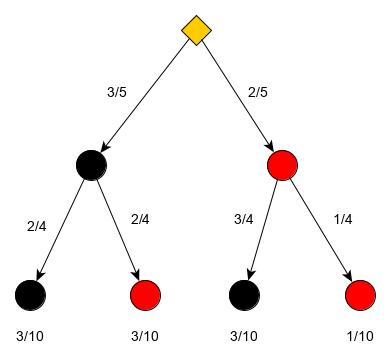
   Baumdiagramm: 5 Bälle, 2 rot (r) und 3 schwarz (s), 2 mal ziehen ohne Zurücklegen

   E = 2. Kugel ist rot \(=\{sr, rr\}\)

   \(Pr[E]=\frac{3}{10}+\frac{1}{10}=\frac{4}{10}=\frac{2}{5}\)

Beispiel: Nachweis für Wk.-Raum

Signalübertragung über Kanal. Erfolgreiche Übertragung mit Wk. p. Mit welcher Wk. braucht man k Versuche bis zu einer erfolgreichen Übertragung?

Definiere Elementarereignisse:

\(\omega_i =\) erfolgreiche Übertragung erstmals beim i-ten Versuch

\(\Omega =\{\omega_1,\omega_2,\omega_3,...\}\)

Übertragung schlägt fehl mit Wk. \(q=1-p\).

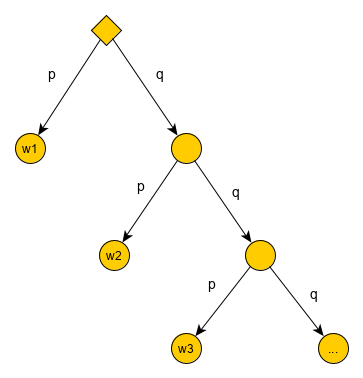
Baumdiagramm: zur Signalübertragung

\(Pr[\omega_i]=q^{i-1}*p\)

\(\sum_{i=1}^\infty Pr[\omega_i]=\sum_{i=1}^\infty q^{i-1}p=p*\sum_{i=0}^\infty q^i=p*\frac{1}{1-q}=p*\frac{1}{p}=1\)

\(\Rightarrow\) Wk.-Raum

Bsp.

Ereignis \(A_k=\) Erfolg in weniger gleich k Versuchen \(=\{\omega_1,\omega_2,...,\omega_k\}\)

\(Pr[A_k]=\sum_{i=1}^k Pr[\omega_i]=\sum_{i=1}^k q^{i-1}p=p*\sum_{i=0}^{k-1}q^i=p*\frac{1-q^k}{1-q}=1-q^k=1- (1-p)^k\)

Anmerkung: \(q^k\) geht exponentiell gegen \(0\). Also geht \(1-(1-p)^k\) exponentiell gegen \(1\).

Eigenschaften

Seien \(A,B \subseteq \Omega\) Ereignisse.

1. \(Pr[\emptyset]=0\), (da \(0\le Pr[\emptyset]\le 1-Pr[\Omega]=0\)) und \(Pr[\Omega]=1\) (nach Definition)

2. \(Pr[\bar A]=1-Pr[A]\)

   \(A \cup \bar A= \Omega \Rightarrow Pr[\bar A] + Pr[A] = Pr[\Omega] = 1\)

3. \(A\subseteq B \Rightarrow Pr[A] \le Pr[B]\)

   \(Pr[B]=\sum_{\omega\in B}Pr[\omega]=\sum_{\omega\in A}Pr[\omega] + \sum_{\omega\in B-A}Pr[\omega] \ge \sum_{\omega\in A}Pr[\omega]=Pr[A]\)

4. \(A \cap B = \emptyset \Rightarrow Pr[A \cup B]=Pr[A] + Pr[B]\)

   Additionssatz: \(\sum_{\omega\in A \cup B}Pr[\omega] = \sum_{\omega\in A}Pr[\omega] + \sum_{\omega\in B}Pr[\omega]\)

   Allgemeiner für \(A_1, A_2, ...\) paarweise disjunkt gilt:

   \[Pr[\bigcup_{i\ge 1}A_i]=\sum_{i\ge 1}Pr[A_i]\]

5. \(Pr[A \cup B]=Pr[A]+Pr[B]-Pr[A \cap B]\)

   Siebformel:

   \begin{align*} \vert A\cup B\vert &= \vert A\vert + \vert B\vert -\vert A\cap B\vert\\ \vert A\cup B \cup C\vert &= \vert A\vert + \vert B\vert +\vert C\vert -(\vert A\cap B\vert + \vert A\cap C\vert + \vert B\cap C\vert) + \vert A\cap B \cap C\vert\\\\ \vert A_1\cup A_2 \cup ... \cup A_n\vert &= \\ = \sum_{i=1}^n \vert A_i \vert - \sum_{1\le i < j \le n} \vert & A_i \cap A_j \vert + \sum_{1\le i<j<k \le n} \vert A_i \cap A_j \cap A_k \vert -+... + (-1)^{n+1}\vert A_1 \cap ... \cap A_n \vert \end{align*}

Beweis: Allgemeine Siebformel

Sei \(a\in A_1 \cup A_2 \cup ... \cup A_n\) beliebig.

Zeige: a wird durch die Formel auf der rechten Seite genau einmal gezählt.

Komme a in m der Mengen \(A_1, A_2,..., A_n\) vor. (\(1\le m \le n\))

• a wird in \(S_1\) m-mal gezählt
• \(\;\;\;\) - “ - \(\;\;\;\;S_2 \;\;{m \choose 2}\)-mal gezählt (=Anzahl Paare aus m Elementen)
• \(\;\;\;\) - “ - \(\;\;\;\;S_k \;\;{m \choose k}\)-mal gezählt
• \(\;\;\;\) - “ - \(\;\;\;\;S_m \;{m \choose m}\)-mal gezählt
• \(\;\;\;\) - “ - \(\;\;\;\;S_n \;\;\;\; 0\)-mal gezählt

\(\Rightarrow a\) wird \({m \choose 1} - {m \choose 2} + {m \choose 3}-+...+(-1)^{m+1}{m \choose m}\) - mal gezählt.

Binomialtheorem: \((x+y)^n=\sum_{k=0}^n{n \choose k}x^k y^{n-k}\)

Setze \(x=-1, \; y=1 ,\; n\ge 1\)

\begin{gather*} (-1+1)^n=0=\sum_{k=0}^n {n \choose k}(-1)^k={n \choose 0}-{n \choose 1}+{n \choose 2}-...+(-1)^n{n \choose n}\\ \Leftrightarrow {n \choose 1}-{n \choose 2}+{n \choose 3}-...+(-1)(-1)^n{n \choose n} = 1 \end{gather*}

\(\Rightarrow a\) wird 1-mal gezählt. (n wird durch m ersetzt und \((-1)(-1)^n = (-1)^{m+1}\))

Folgerung:

\begin{gather*} Pr[A_1\cup A_2 \cup ... \cup A_n] = \\ \sum_{i=1}^n Pr[A_i] - \sum_{1\le i < j \le n} Pr[ A_i \cap A_j] + \sum_{1\le i<j<k \le n} Pr[ A_i \cap A_j \cap A_k] -+... + (-1)^{n+1}Pr[ A_1 \cap ... \cap A_n] \end{gather*}

Beispiel:

n Seeleute kehren betrunken auf ihr Schiff zurück. Jeder fällt zufällig in eine Koje. Mit welcher Wk. liegt keiner in seiner eigenen Koje? (Komplementär: Min. ein Seemann liegt in seiner Koje)

Seemann i gehört Koje i, \(i=1,2,...,n\). Jede Verteilung der Seeleute auf die Kojen ist eine Permutation \(\pi \in S_n\), d.h. \(\pi:[n] \rightarrow [n]\).

Ereignis \(A_i=\) Seemann i liegt in seiner Koje i, d.h. \(A_i=\{\pi\in S_n \mid \pi (i)=i\}\)

\(\vert S_n \vert = n!\)

\(\vert A_i \vert = (n-1)!\), da n-1 Seeleute beliebig auf n-1 Kojen verteilt werden.

\(Pr[\pi]=\frac{1}{\vert S_n\vert}=\frac{1}{n!}\) (Laplace-prinzip)

\(Pr[A_i]=\frac{\vert A_i\vert}{\vert S_n\vert}=\frac{(n-1)!}{n!}=\frac{1}{n}\)

\(A=A_1\cup A_2\cup ... \cup A_n =\) min ein Seemann liegt in der richtigen Koje.

\begin{align*} i<j: \;\;\vert A_i \cap A_j\vert &= (n-2)! \\ i<j<k: \;\;\vert A_i \cap A_j \cap A_k\vert &= (n-3)! \\ ...\\ \vert A_1 \cap A_2\cap ... \cap A_n\vert &= (n-n)!=0!=1 \\ \Rightarrow \vert A_1\cup A_2\cup ... \cup A_n \vert &= \sum_{i=1}^n \vert A_i \vert - \sum_{1\le i < j \le n} \vert A_i \cap A_j \vert + \sum_{1\le i<j<k \le n} \vert A_i \cap A_j \cap A_k \vert -+... + (-1)^{n+1}\vert A_1 \cap ... \cap A_n \vert\\ &= \sum_{k=1}^n (-1)^{k+1} {n \choose k}(n-k)!\\ &= \sum_{k=1}^n (-1)^{k+1} \frac{n!}{k!(n-k)!} * (n-k)!\\ &= n!*\sum_{k=1}^n \frac{(-1)^{k+1}}{k!}\\ \Rightarrow Pr[A]&=\frac{\vert A\vert}{\vert S_n\vert}=\frac{n!*\sum_{k=1}^n \frac{(-1)^{k+1}}{k!}}{n!}= \sum_{k=1}^n \frac{(-1)^{k+1}}{k!}\\ Pr[\bar A]&=1-Pr[A]=1-\sum_{k=1}^n \frac{(-1)^{k+1}}{k!}=\sum_{k=0}^n \frac{(-1)^{k}}{k!} \xrightarrow{n\to\infty}\frac{1}{e} \approx 0.36788 \end{align*}

Hinweis: \(\sum_{0}^\infty \frac{1}{k!}=e\) und \(\sum_{0}^\infty \frac{x^k}{k!}=e^x\)

\(Pr[\bar A]\) ist die Wk., dass keiner in seiner Koje liegt.

Zusammenfassung: Wahrscheinlichkeitsräume

Wahrscheinlichkeitsraum: \(\Omega =\{\omega_1, \omega_2, \omega_3, ...\}\)

Elementarereignisse: \(\omega_1, \omega_2, \omega_3, ...\)

Summe aller Elementarergeinissen: \(\sum_{\omega_i\in \Omega} Pr[\omega_i] = 1\)

Ereignis \(E\subseteq\Omega\): \(Pr[E] = \sum_{\omega\in E} Pr[\omega]\)

E tritt ein, sobald ein Elementarereigniss eintritt.

komplementär Ereignis: \(\bar E=\Omega-E\)

Laplace Experiment: \(Pr[E]=\frac{\vert E\vert}{\vert\Omega\vert}\)

Eigenschaften: Seien \(A,B \subseteq \Omega\) Ereignisse.

• \(Pr[\emptyset]=0\)
• \(Pr[\Omega]=1\)
• \(Pr[\bar A]=1-Pr[A]\)
• \(A\subseteq B \Rightarrow Pr[A] \le Pr[B]\)

Additionssatz: \(A_1, A_2, ...\) paarweise disjunkt gilt: \(Pr[\bigcup_{i\ge 1}A_i]=\sum_{i\ge 1}Pr[A_i]\)

Allgemeine Siebformel:

\begin{align*} \vert A_1\cup A_2 \cup ... \cup A_n\vert = &\sum_{i=1}^n \vert A_i \vert \\ &- \sum_{1\le i < j \le n} \vert A_i \cap A_j \vert \\ &+ \sum_{1\le i<j<k \le n} \vert A_i \cap A_j \cap A_k \vert\\ &-+... \\ &+ (-1)^{n+1}\vert A_1 \cap ... \cap A_n \vert \end{align*}

Fußnoten

[1]	Aufzählbar und isolierte Objekte

[2]	Unendlich viele Objekte möglich